Fixed-Point Iteration Method

Fixed-Point

The number p is a fixed point for a given function g if

                                    g( p) = p.

A fixed point for a function is a number at which the value of the function does not change when the function is applied.

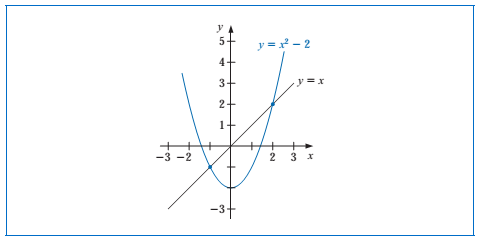
Example 1: Determine any fixed points of the function g(x) = x²-2

Solution:      A fixed point p for g has the property that

                                                                p = g( p) =p²− 2

which implies that

                                                  0 = p² − p − 2 = ( p + 1)( p − 2).

A fixed point for g occurs precisely when the graph of y = g(x) intersects the graph of y = x, so g has two fixed points, one at p = −1 and the other at p = 2. These are shown in the following figure.

Theorem:

(i) If g ∈ C[a, b] and g(x) ∈ [a, b] for all x ∈ [a, b], then g has at least one fixed point in [a, b].

(ii) If, in addition, g(x) exists on (a, b) and a positive constant k < 1 exists with |g(x)| ≤ k, for all 

     x ∈ (a, b), then there is exactly one fixed point in [a, b]. 

Example 2:  Show that g(x) = (x² − 1)/3 has a unique fixed point on the interval [−1, 1].

Fixed-Point Iteration

Let g ∈ C[a, b] be such that g(x) ∈ [a, b], for all x in [a, b]. Suppose, in addition, that g exists on (a, b) and that a constant 0 < k < 1 exists 

Then for any number p0 in [a, b], the sequence defined by

                                                                p_n = g( p_n-1), n ≥ 1,

converges to the unique fixed point p in [a, b]. This technique is called fixed-point, or functional iteration. The procedure is illustrated in the following figure.

Maple Solution:

restart;

with(Student[NumericalAnalysis]);

f := x-cos(x);

                           x - cos(x)

plot(f, x = 0 .. 4);

g1 := cos(x);

                             cos(x)

plot([f, g1, x], x = 0 .. 5, color = [black, red, blue]);