Fixed-Point Iteration Method
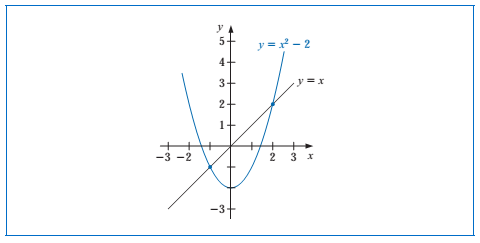
Fixed-Point The number p is a fixed point for a given function g if g( p) = p . A fixed point for a function is a number at which the value of the function does not change when the function is applied. Example 1 : Determine any fixed points of the function g(x) = x 2 -2 Solution : A fixed point p for g has the property that p = g( p) = p 2 − 2 which implies that ...


